L'outil de tracé vous permet de créer des graphiques détaillés et dynamiques sur une grille simple. Associé à l'outil d'équation, il devient un puissant outil de traçage avec support pour les équations cartésiennes, polaires et paramétrées.
Outil de tracé
Ajouter une grille de tracé
Pour commencer, ajoutez une grille de tracé à votre espace de travail :
- Cliquez sur le bouton Graphique dans la barre d'outils (raccourci : H) pour sélectionner l'outil de tracé.
- Dessinez un rectangle sur le tableau. Une grille avec les axes x et y apparaîtra.
Vous pouvez dessiner manuellement des graphiques sur la grille, mais cela est moins amusant. Il est beaucoup plus puissant de tracer des équations dessus. Nous allons apprendre à le faire tout de suite.
Tracer des équations
Pour tracer une équation, suivez ces étapes :
- Utilisez l'outil d'équation pour entrer une équation (par exemple, y = 2x^3).
- Sélectionnez l'équation et cliquez sur le bouton Tracer l’équation dans les options de formule de la barre d’outils (ou dans la barre flottante si elle est activée). Cela crée un objet graphique et lie l’équation au graphique.
- Le graphique de l'équation que vous avez écrite sera automatiquement tracé sur la grille.
- Une fois la grille ajoutée, vous pouvez la redimensionner ou la déplacer pour ajuster la disposition de votre espace de travail.
Les modifications apportées à l'équation sont immédiatement reflétées sur le graphique. Vous pouvez également tracer plusieurs équations sur le même graphique en les liant manuellement au graphique à l'aide de l'outil de connexion.

Définir les plages de paramètres
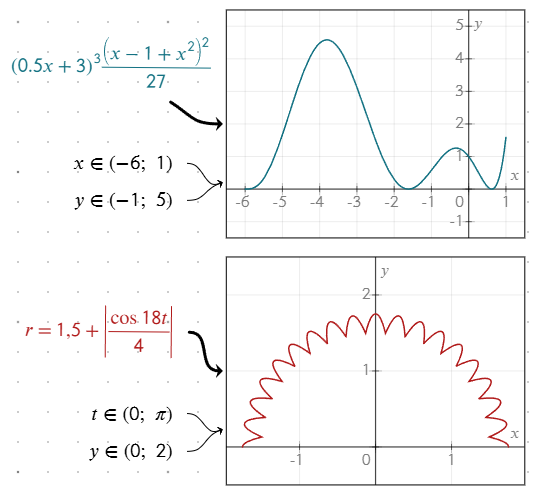
Vous pouvez définir une plage spécifique pour votre graphique à l'aide d'une notation d'intervalle. Cela vous permet de contrôler la portion du graphique tracée.
Entrez une plage sous la forme d'une équation comme x ∈ (-6; 2). Le graphique sera limité à la plage spécifiée. Pour obtenir le symbole ∈, tapez \in[espace] ou trouvez le symbole dans la barre d'outils d'équation.
Par exemple, en coordonnées polaires, vous pouvez limiter la plage angulaire à t ∈ (0; π) pour tracer un demi-cercle. De même, pour les équations paramétrées, vous pouvez limiter la plage du paramètre pour obtenir un segment spécifique du graphique.
Si aucune plage n'est définie, l'outil utilise des limites par défaut pour la variable ou le paramètre en fonction du type de graphique. Par exemple, pour les graphiques cartésiens, les plages des variables x et y dépendent de la taille de l'objet graphique. En coordonnées polaires, la plage de la variable est de 0 à 2π, et pour les équations paramétrées, la plage par défaut est t ∈ (-5; 5).
Personnaliser l’apparence du graphique
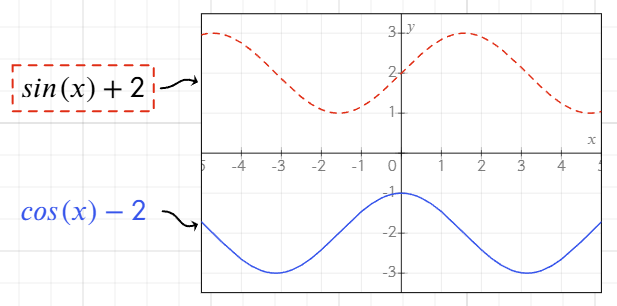
Vous pouvez personnaliser les lignes du graphique en modifiant l'apparence de l'équation :
- Ajoutez une bordure autour de l'équation pour correspondre au style de la ligne du graphique.
- Changez la couleur du texte de l'équation pour ajuster la couleur de la ligne sur le graphique.
Si aucune bordure n'est appliquée, la couleur du texte détermine par défaut la couleur de la ligne.
Types d’équations pris en charge
L'outil de tracé prend en charge plusieurs types d'équations :
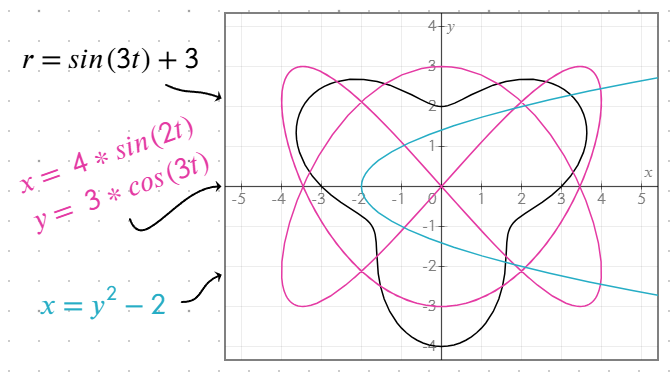
- Équations cartésiennes : Soit
ycomme fonction dex, soitxcomme fonction dey. - Équations polaires : Utilisez des équations qui calculent
rcomme fonction det,thetaouθ. Par exemple,r = sin(t) + 2. Les graphiques sont tracés sur la plage[0, 2π]. L'équation se comporte de manière identique quel que soit le nom de la variable utilisée. - Équations paramétrées : Définissez
xetycomme des fonctions du même paramètre sur des lignes distinctes dans le même objet d'équation, par exemple :
x = 4 * sin(2t)
y = 3 * cos(3t)
Utiliser des variables dans les équations
Vous pouvez définir des variables dans les équations et les réutiliser dans d'autres. Par exemple : a = x^2, y = 0.2a - 1/a.
Le graphique est mis à jour dynamiquement à chaque modification de la variable ou des équations dépendantes.
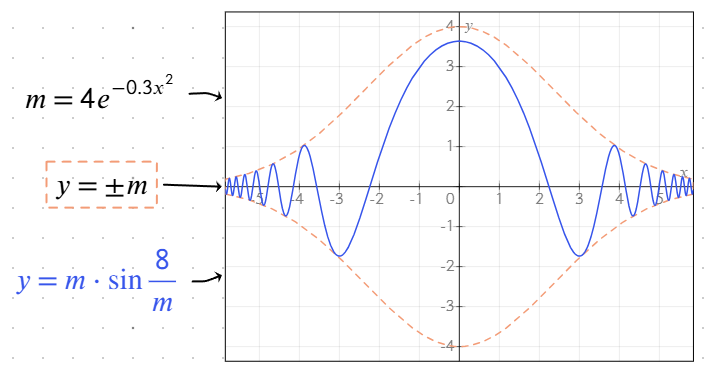
Fonctions prises en charge
L'outil de tracé de graphes comprend une variété de fonctions intégrées pour simplifier la saisie des équations et améliorer la visualisation.
Fonctions trigonométriques
- Standard :
sin,cos,tan,csc,sec,cot - Fonctions inverses (arc) :
arcsin,arccos,arctan - Fonctions hyperboliques :
sinh,cosh,tanh,csch,sech,coth
Fonctions logarithmiques
log(x): Logarithme en base 10ln(x): Logarithme naturel (base e)
Autres fonctions
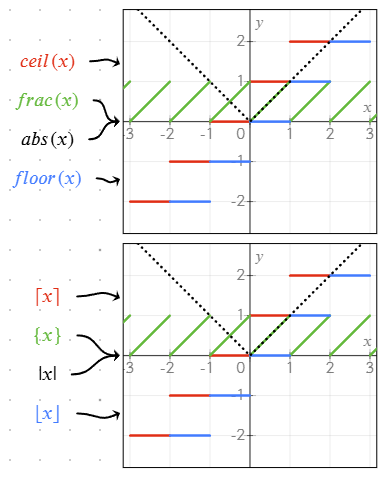
sqrt(x): Racine carréeabs(x)ou|x|: Valeur absoluefrac(x)ou{x}: Partie fractionnaire d'un nombrefloor(x)ou⌊x⌋: Arrondi à l'entier inférieurceil(x)ou⌈x⌉: Arrondi à l'entier supérieurmin(a; b),max(a; b): Minimum/maximum de deux valeurs ou plus
Ces fonctions peuvent être combinées dans les équations pour créer des graphiques et des calculs plus complexes.
Définition et utilisation des fonctions personnalisées
L'outil de tracé prend en charge la définition de fonctions en utilisant la notation f(x) = ..., ce qui permet de réutiliser facilement des expressions dans plusieurs équations.
Pour définir une fonction, utilisez le format : f(x) = cos(2x) + sin(x)
Utilisation des fonctions dans les équations
Une fois définie, une fonction peut être référencée dans d'autres équations : g(x) = f(x) + 5
Si une fonction est définie avec f(x) = ..., elle est tracée sur le graphique. D'autres variations (par exemple, g(t)) ne sont pas tracées mais peuvent être utilisées dans les calculs.
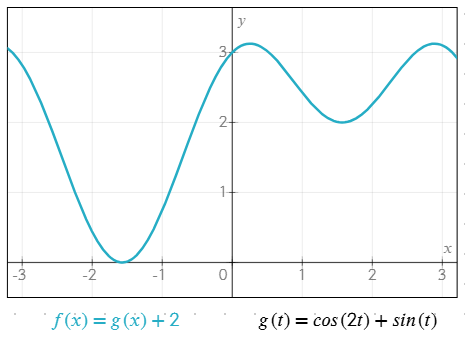
Exemple de plusieurs fonctions travaillant ensemble
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Les fonctions personnalisées aident à simplifier les équations, éviter les répétitions et gérer plus facilement les expressions complexes.
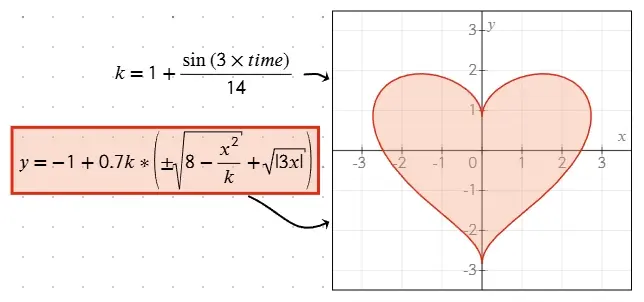
Animer des graphiques avec la variable 'time'
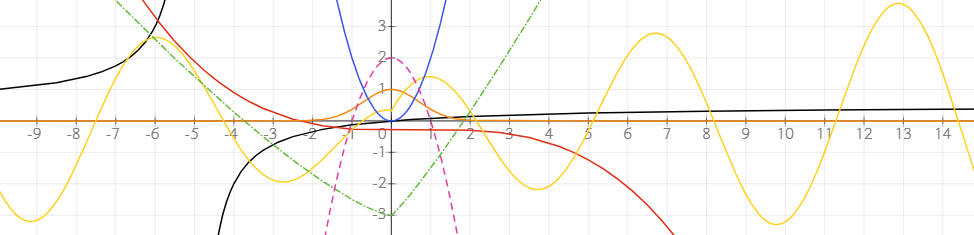
Utilisez la variable spéciale time pour créer des graphiques animés. La variable time augmente de 1 chaque seconde, vous permettant de simuler un mouvement ou des changements périodiques dans vos équations.
Par exemple : r = sin(5 * time) + 2 crée un cercle pulsant qui se met à jour en temps réel.
Sur l'image à droite, vous pouvez voir une équation un peu plus complexe utilisant la variable temps.
Utiliser des variables prédéfinies
L'outil de tracé comprend plusieurs constantes prédéfinies qui peuvent simplifier la création d'équations. Ces constantes sont :
piouπ: Constante mathématique π (~3.14159).e: Nombre d'Euler (~2.71828).infinityou∞, bien qu'elle soit généralement moins utile pour tracer des graphiques finis.
Gérer les équations avec plusieurs solutions
Utiliser ± pour des solutions symétriques
Insérez le symbole ± (ou +-, qui est automatiquement converti en ±) dans l'équation pour tracer simultanément les résultats positifs et négatifs. Par exemple, y = ±sqrt(x) trace à la fois y = sqrt(x) et y = -sqrt(x).
Spécifier plusieurs valeurs
Vous pouvez spécifier plusieurs valeurs ou sous-équations dans un seul objet d'équation en utilisant un format de liste ou plusieurs lignes :
- Listes entre crochets : Utilisez
;comme séparateur dans des crochets pour définir plusieurs valeurs. Par exemple :y = (1; -1) * xtracera à la foisy = xety = -x. - Lignes séparées : Appuyez sur Entrée dans l'éditeur d'équation pour ajouter plusieurs sous-équations sur des lignes différentes. Chaque ligne est traitée comme une solution indépendante.
Ces méthodes permettent une création flexible de graphiques avec plusieurs branches ou solutions, facilitant la visualisation des relations complexes.
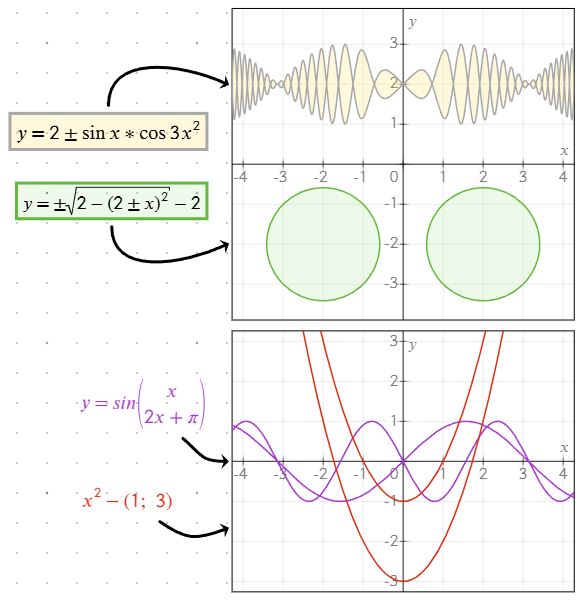
Résolution des problèmes de traçage d’équations
Si une équation ne se trace pas, cela est probablement dû à l'une des raisons suivantes :
- Il y a une erreur dans la syntaxe de l'équation (par exemple, un opérateur manquant ou un symbole invalide).
- La plage de la variable (par exemple,
xout) est mal définie ou non spécifiée. - L'équation peut être intrinsèquement indéfinie dans certaines régions (par exemple, une division par zéro).
Pour résoudre ces problèmes :
- Vérifiez votre équation pour détecter des fautes de frappe ou des erreurs de format.
- Si vous avez spécifié une plage, assurez-vous que l'intervalle est valide et pertinent pour votre équation.
- Essayez de retaper l'équation pour vous assurer que tous les symboles et opérateurs sont correctement saisis.
Si les problèmes persistent, testez l'équation isolément pour confirmer sa validité.
Considérations de performance
Lorsque vous travaillez avec des graphiques complexes ou dynamiques, les performances peuvent être impactées. Gardez à l'esprit les conseils suivants pour maintenir une expérience fluide :
- Équations complexes : Les graphiques avec des calculs intensifs (par exemple, des fonctions trigonométriques imbriquées ou de grandes plages) peuvent ralentir le rendu, en particulier lorsqu'ils sont combinés avec des animations.
- Oscillations rapides : Les équations avec des oscillations à haute fréquence (par exemple,
y = tan(1/x)) peuvent être mal tracées près de leurs points de rupture en raison des limitations de rendu. Pour réduire cela, limitez la plage ou simplifiez l'équation si possible. - Fluidité de l’animation : Si vous utilisez la variable
timepour des animations, assurez-vous que vos équations n'effectuent pas de recalculs excessifs à chaque image pour maintenir un mouvement fluide.
Pour de meilleurs résultats, envisagez de décomposer des graphiques trop complexes en composants plus simples ou d'utiliser des plages plus étroites pour réduire la charge de calcul.
Un trop grand nombre de graphiques visibles à l'écran peut également affecter négativement les performances. Évitez d'ajouter trop de graphiques rapprochés pour une expérience plus fluide.