Инструмент построения графиков позволяет создавать подробные и динамичные графики на простой сетке. В сочетании с инструментом уравнений он становится мощным инструментом для построения графиков уравнений с поддержкой декартовых, полярных и параметрических уравнений.
Инструмент построения графиков
Добавление сетки графика
Чтобы начать, добавьте сетку графика в ваше рабочее пространство:
- Нажмите кнопку График на панели инструментов (ярлык: H), чтобы выбрать инструмент построения графиков.
- Нарисуйте прямоугольник на доске. Появится сетка с осями x и y.
Вы можете вручную рисовать графики на сетке, но это не так интересно. Намного мощнее — строить графики уравнений. Давайте сразу научимся, как это делать.
Построение графиков уравнений
Чтобы построить график уравнения, выполните следующие шаги:
- Используйте инструмент уравнений, чтобы ввести уравнение (например, y = 2x^3).
- Выделите уравнение и нажмите кнопку Построить график в параметрах формулы на панели инструментов (или на плавающей панели, если она включена). Это создаст объект графика и свяжет уравнение с графиком.
- График введённого уравнения автоматически отобразится на сетке.
- После добавления сетки вы можете изменить её размер или переместить, чтобы настроить макет рабочего пространства.
Изменения в уравнении сразу же отображаются на графике. Вы также можете построить несколько уравнений на одном графике, если вручную свяжете их с графиком с помощью инструмента соединения.

Определение диапазонов параметров
Вы можете задать определённый диапазон для графика, используя обозначение интервала. Это позволяет контролировать, какая часть графика будет построена.
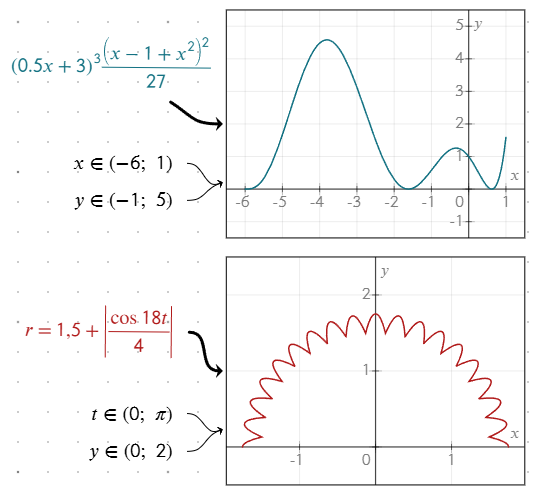
Введите диапазон в виде уравнения, например, x ∈ (-6; 2). График будет ограничен указанным диапазоном. Чтобы получить символ ∈, введите \in[пробел] или найдите символ в панели инструментов уравнений.
Например, в полярных координатах вы можете ограничить диапазон углов t ∈ (0; π), чтобы построить полуокружность. Аналогично, для параметрических уравнений вы можете ограничить диапазон параметра, чтобы построить определённый сегмент графика.
Если диапазон не задан, инструмент использует значения по умолчанию для переменной или параметра в зависимости от типа графика. Например, в декартовых графиках диапазоны x и y зависят от размера объекта графика. В полярных графиках диапазон переменной составляет от 0 до 2π, а в параметрических уравнениях диапазон по умолчанию — t ∈ (-5; 5).
Настройка внешнего вида графика
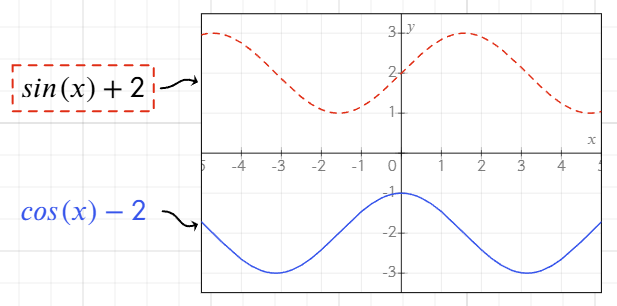
Вы можете настроить линии графика, изменяя стиль уравнения:
- Добавьте рамку вокруг уравнения, чтобы стиль соответствовал линии графика.
- Измените цвет текста уравнения, чтобы настроить цвет линии на графике.
Если рамка не добавлена, цвет текста по умолчанию определяет цвет линии.
Поддерживаемые типы уравнений
Инструмент построения графиков поддерживает различные типы уравнений:
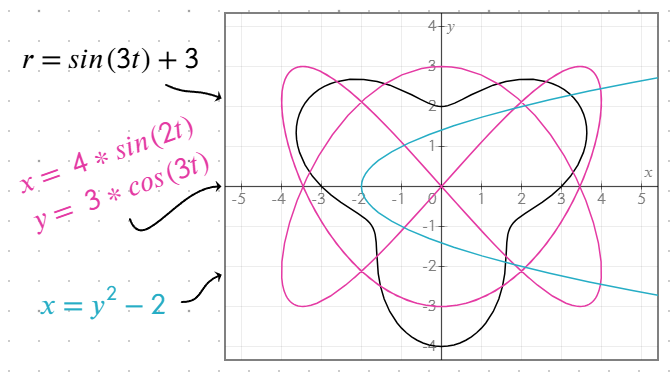
- Декартовы уравнения:
yкак функцияxилиxкак функцияy. - Полярные уравнения: Используйте уравнения, вычисляющие
rкак функциюt,thetaилиθ. Например,r = sin(t) + 2. Графики строятся в диапазоне[0, 2π]. Уравнение ведёт себя одинаково, независимо от имени используемой переменной. - Параметрические уравнения: Определите
xиyкак функции одного и того же параметра на отдельных строках в одном и том же объекте уравнения, например:
x = 4 * sin(2t)
y = 3 * cos(3t)
Использование переменных в уравнениях
Вы можете задавать переменные в уравнениях и повторно использовать их в других. Например: a = x^2, y = 0.2a - 1/a.
График динамически обновляется каждый раз при изменении переменной или зависимых уравнений.
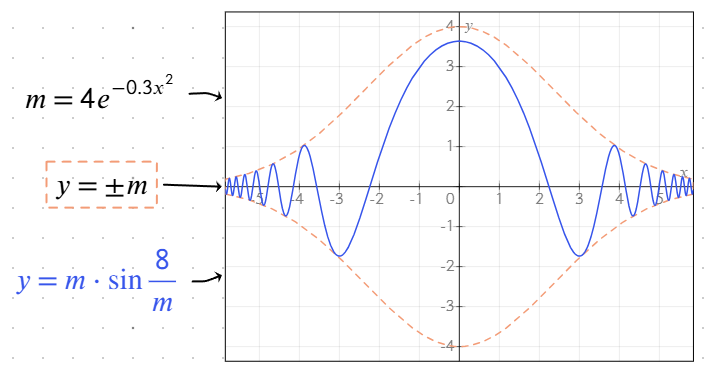
Поддерживаемые функции
Инструмент построения графиков включает в себя различные встроенные функции, упрощающие ввод уравнений и улучшающие визуализацию.
Тригонометрические функции
- Стандартные:
sin,cos,tan,csc,sec,cot - Обратные (аркфункции):
arcsin,arccos,arctan - Гиперболические функции:
sinh,cosh,tanh,csch,sech,coth
Логарифмические функции
log(x): Десятичный логарифмln(x): Натуральный логарифм (по основанию e)
Другие функции
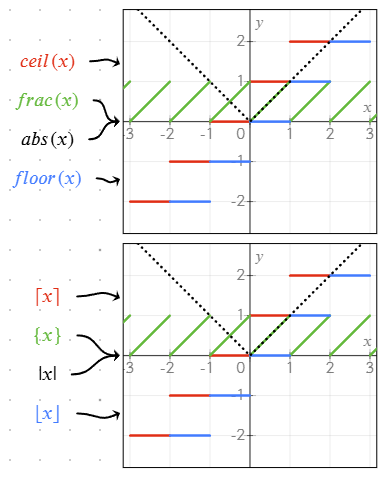
sqrt(x): Квадратный кореньabs(x)или|x|: Модуль числаfrac(x)или{x}: Дробная часть числаfloor(x)или⌊x⌋: Округление вниз до ближайшего целогоceil(x)или⌈x⌉: Округление вверх до ближайшего целогоmin(a; b),max(a; b): Минимум/максимум из двух или более значений
Эти функции можно комбинировать в уравнениях для создания более сложных графиков и вычислений.
Определение и использование пользовательских функций
Инструмент построения графиков поддерживает определение функций с использованием нотации f(x) = ..., что облегчает повторное использование выражений в нескольких уравнениях.
Чтобы определить функцию, используйте формат: f(x) = cos(2x) + sin(x)
Использование функций в уравнениях
После определения функция может быть использована в других уравнениях: g(x) = f(x) + 5
Если функция определена как f(x) = ..., она отображается на графике. Другие варианты (например, g(t)) не отображаются, но могут использоваться в вычислениях.
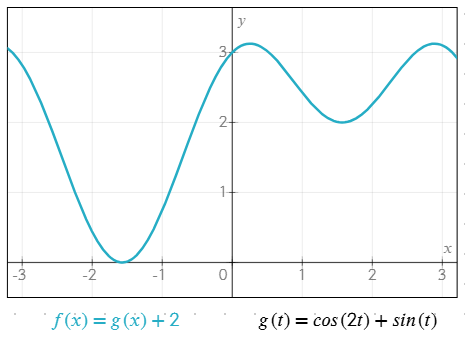
Пример работы нескольких функций вместе
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Пользовательские функции помогают упростить уравнения, избежать повторений и легче управлять сложными выражениями.
Анимация графиков с помощью переменной 'time'
Используйте специальную переменную time, чтобы создавать анимированные графики. Переменная time увеличивается на 1 каждую секунду, что позволяет моделировать движение или периодические изменения в уравнениях.
Например: r = sin(5 * time) + 2 создаёт пульсирующий круг, который обновляется в реальном времени.
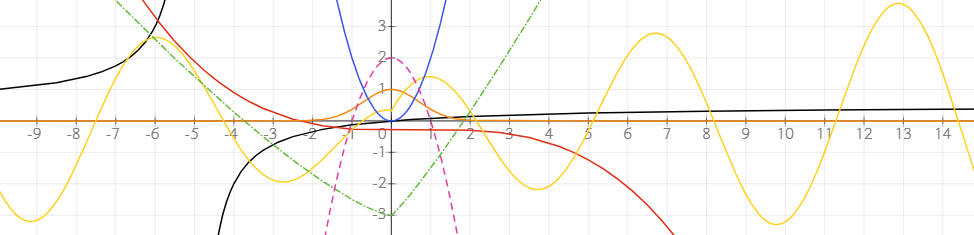
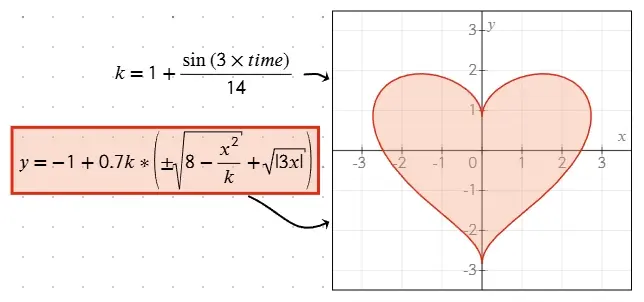
На изображении справа показано более сложное уравнение, использующее переменную времени.
Использование предопределённых переменных
Инструмент построения графиков включает несколько предопределённых констант, которые могут упростить создание уравнений. Эти константы:
piилиπ: Математическая константа π (~3.14159).e: Число Эйлера (~2.71828).infinityили∞, хотя для построения конечных графиков она используется редко.
Работа с уравнениями с несколькими решениями
Использование ± для симметричных решений
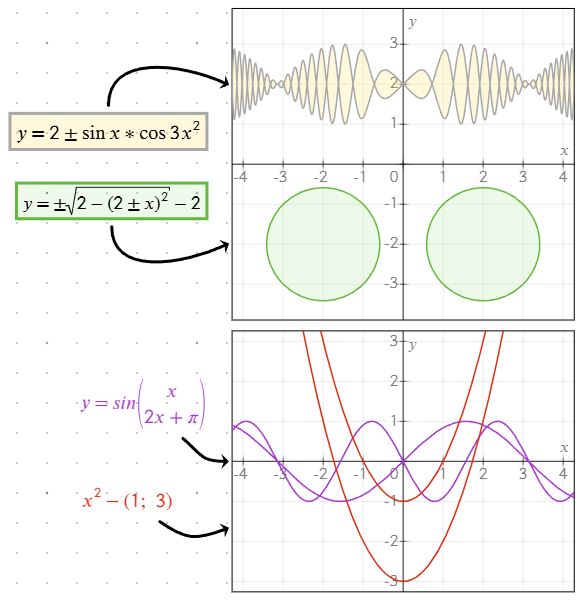
Вставьте символ ± (или +-, который автоматически преобразуется в ±), чтобы одновременно построить положительные и отрицательные решения. Например: y = ±sqrt(x) строит как y = sqrt(x), так и y = -sqrt(x).
Указание нескольких значений
Вы можете указать несколько значений или подуравнений в одном объекте уравнения, используя формат списка или несколько строк:
- Списки в скобках: Используйте
;как разделитель в скобках, чтобы задать несколько значений. Например:y = (1; -1) * xпостроит какy = x, так иy = -x. - Отдельные строки: Нажмите Enter в редакторе уравнений, чтобы добавить несколько подуравнений на разных строках. Каждая строка обрабатывается как независимое решение.
Эти методы позволяют гибко создавать графики с несколькими ветвями или решениями, облегчая визуализацию сложных зависимостей.
Устранение неполадок построения графиков уравнений
Если уравнение не строится, это может быть связано с одной из следующих причин:
- Ошибка в синтаксисе уравнения (например, отсутствующий оператор или недопустимый символ).
- Диапазон переменной (например,
xилиt) неправильно задан или не указан. - Уравнение может быть не определено в некоторых областях (например, деление на ноль).
Чтобы устранить эти проблемы:
- Проверьте уравнение на наличие опечаток или ошибок форматирования.
- Если вы задали диапазон, убедитесь, что интервал корректен и релевантен для вашего уравнения.
- Попробуйте заново ввести уравнение, чтобы убедиться, что все символы и операторы введены правильно.
Если проблемы сохраняются, протестируйте уравнение отдельно, чтобы убедиться в его правильности.
Особенности производительности
При работе со сложными или динамическими графиками производительность может снизиться. Чтобы обеспечить плавность работы, обратите внимание на следующие советы:
- Сложные уравнения: Графики с вычислительно сложными расчётами (например, вложенные тригонометрические функции или большие диапазоны) могут замедлить отрисовку, особенно при использовании анимации.
- Быстрые колебания: Уравнения с высокочастотными колебаниями (например,
y = tan(1/x)) могут быть неточно построены рядом с точками разрыва из-за ограничений отрисовки. Чтобы это уменьшить, ограничьте диапазон или упростите уравнение, если это возможно. - Плавность анимации: Если вы используете переменную
timeдля анимации, убедитесь, что ваши уравнения не выполняют чрезмерные пересчёты в каждом кадре, чтобы сохранить плавность движения.
Для достижения наилучших результатов рассмотрите возможность разбиения слишком сложных графиков на более простые компоненты или использования более узких диапазонов для снижения вычислительной нагрузки.
Слишком большое количество графиков на экране также негативно влияет на производительность. Избегайте добавления слишком большого числа графиков в одном месте для более плавной работы.