Інструмент побудови графіків дозволяє створювати детальні та динамічні графіки на простій сітці. У поєднанні з інструментом рівнянь він стає потужним засобом для побудови графіків рівнянь із підтримкою декартових, полярних та параметричних рівнянь.
Інструмент побудови графіків
Додавання сітки графіка
Щоб почати, додайте сітку графіка до вашого робочого простору:
- Натисніть кнопку Графік на панелі інструментів (комбінація клавіш: H), щоб вибрати інструмент побудови графіків.
- Намалюйте прямокутник на дошці. З’явиться сітка з осями x та y.
Ви можете вручну малювати графіки на сітці, але це не так цікаво. Набагато зручніше побудувати графіки рівнянь на сітці. Ми навчимося це робити просто зараз.
Побудова графіків рівнянь
Щоб побудувати графік рівняння, виконайте наступні дії:
- Використайте інструмент рівнянь, щоб ввести рівняння (наприклад, y = 2x^3).
- Виберіть рівняння і натисніть кнопку Побудувати графік у параметрах формули на панелі інструментів (або у плаваючій панелі, якщо вона увімкнена). Це створить об’єкт графіка та зв’яже рівняння з графіком.
- Графік введеного рівняння автоматично буде побудовано на сітці.
- Після додавання сітки ви можете змінити її розмір або перемістити, щоб налаштувати макет робочого простору.
Зміни у рівнянні миттєво відображаються на графіку. Ви також можете побудувати декілька рівнянь на одному графіку, якщо вручну зв’яжете їх із графіком за допомогою інструмента з’єднання.

Визначення діапазонів параметрів
Ви можете визначити конкретний діапазон для вашого графіка за допомогою інтервальної нотації. Це дозволяє контролювати, яка частина графіка буде побудована.
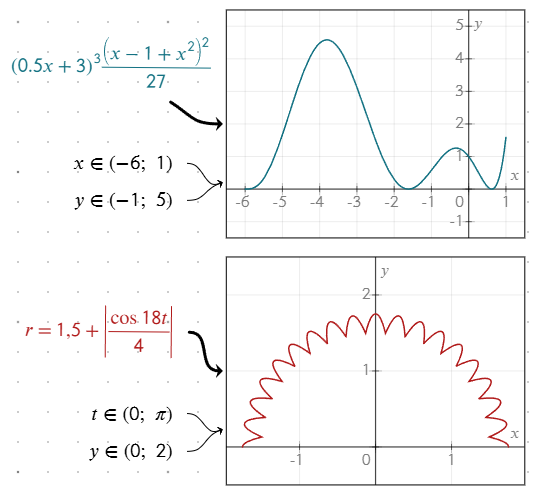
Введіть діапазон у вигляді рівняння, наприклад, x ∈ (-6; 2). Графік буде обмежений вказаним діапазоном. Щоб отримати символ ∈, введіть \in[пробіл] або знайдіть символ у панелі інструментів рівнянь.
Наприклад, у полярних координатах ви можете обмежити кутовий діапазон до t ∈ (0; π), щоб побудувати півколо. Аналогічно, для параметричних рівнянь ви можете обмежити діапазон параметра, щоб побудувати певний сегмент графіка.
Якщо діапазон не визначений, інструмент використовує стандартні межі для змінної або параметра, залежно від типу графіка. Наприклад, у декартових графіках діапазони x і y залежать від розміру об’єкта графіка. У полярних графіках діапазон змінної становить від 0 до 2π, а для параметричних рівнянь стандартний діапазон — t ∈ (-5; 5).
Налаштування вигляду графіка
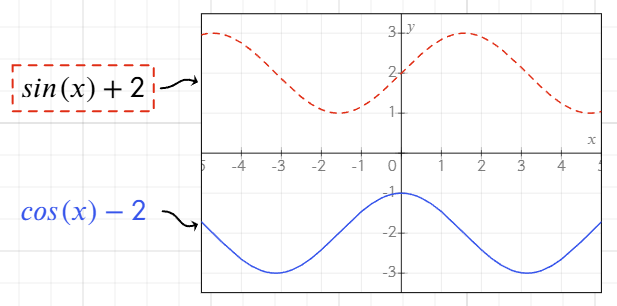
Ви можете стилізувати лінії графіка, змінюючи вигляд рівняння:
- Додайте рамку навколо рівняння, щоб стиль відповідав лінії графіка.
- Змініть колір тексту рівняння, щоб налаштувати колір лінії на графіку.
Якщо рамка не додана, колір тексту за замовчуванням визначає колір лінії.
Підтримувані типи рівнянь
Інструмент побудови графіків підтримує різні типи рівнянь:
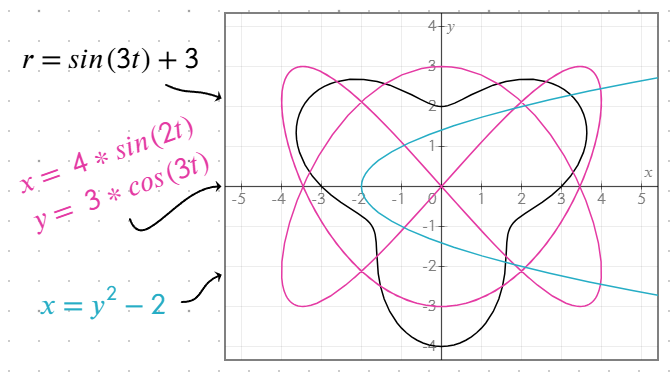
- Декартові рівняння:
yяк функціяxабоxяк функціяy. - Полярні рівняння: Використовуйте рівняння, які обчислюють
rяк функціюt,thetaабоθ. Наприклад,r = sin(t) + 2. Графіки будуються в діапазоні[0, 2π]. Рівняння працює однаково, незалежно від імені змінної. - Параметричні рівняння: Визначте
xіyяк функції одного і того ж параметра на окремих рядках у тому ж об’єкті рівняння, наприклад:
x = 4 * sin(2t)
y = 3 * cos(3t)
Використання змінних у рівняннях
Ви можете визначати змінні в рівняннях і повторно використовувати їх в інших рівняннях. Наприклад: a = x^2, y = 0.2a - 1/a.
Графік динамічно оновлюється щоразу, коли змінюється змінна або залежні рівняння.
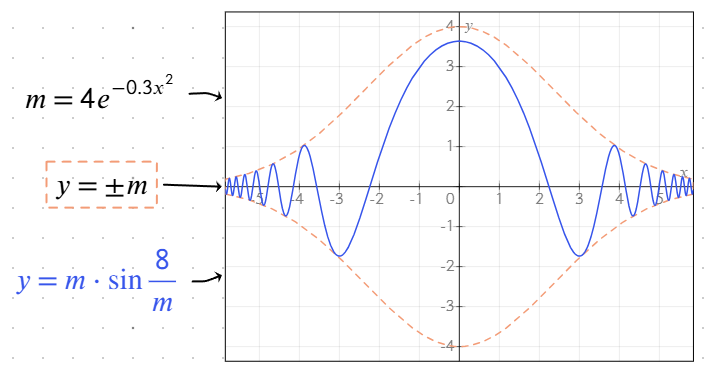
Підтримувані функції
Інструмент побудови графіків містить різні вбудовані функції, що спрощують введення рівнянь та покращують візуалізацію.
Тригонометричні функції
- Стандартні:
sin,cos,tan,csc,sec,cot - Обернені (аркфункції):
arcsin,arccos,arctan - Гіперболічні функції:
sinh,cosh,tanh,csch,sech,coth
Логарифмічні функції
log(x): Десятковий логарифмln(x): Натуральний логарифм (за основою e)
Інші функції
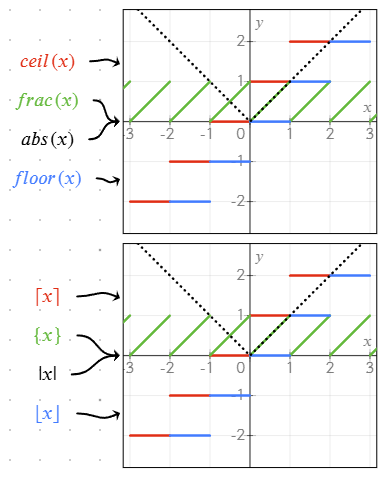
sqrt(x): Квадратний коріньabs(x)або|x|: Модуль числаfrac(x)або{x}: Дробова частина числаfloor(x)або⌊x⌋: Округлення вниз до найближчого цілогоceil(x)або⌈x⌉: Округлення вгору до найближчого цілогоmin(a; b),max(a; b): Мінімальне/максимальне значення серед двох або більше
Ці функції можна комбінувати у рівняннях для створення складніших графіків і розрахунків.
Визначення та використання користувацьких функцій
Інструмент побудови графіків підтримує визначення функцій за допомогою нотації f(x) = ..., що дозволяє повторно використовувати вирази у кількох рівняннях.
Щоб визначити функцію, використовуйте формат: f(x) = cos(2x) + sin(x)
Використання функцій у рівняннях
Після визначення функція може бути використана в інших рівняннях: g(x) = f(x) + 5
Якщо функція визначена як f(x) = ..., вона відображається на графіку. Інші варіації (наприклад, g(t)) не відображаються, але можуть використовуватися в обчисленнях.
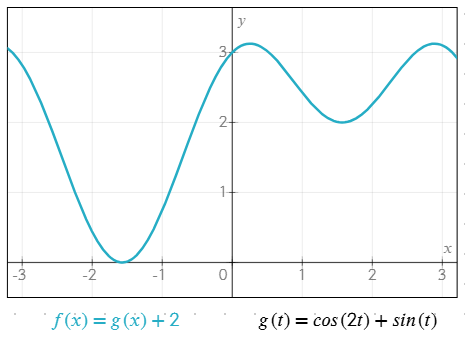
Приклад кількох функцій, що працюють разом
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Користувацькі функції допомагають спрощувати рівняння, уникати повторень і легше керувати складними виразами.
Анімування графіків за допомогою змінної 'time'
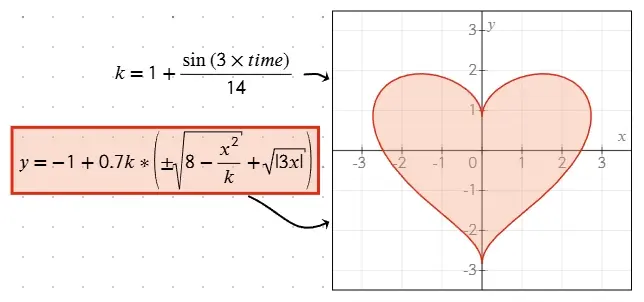
Використовуйте спеціальну змінну time, щоб створювати анімовані графіки. Змінна time збільшується на 1 кожну секунду, дозволяючи моделювати рух або періодичні зміни в рівняннях.
Наприклад: r = sin(5 * time) + 2 створює пульсуюче коло, яке оновлюється в реальному часі.
На зображенні праворуч ви бачите трохи складніше рівняння, яке використовує змінну час.
Використання попередньо визначених змінних
Інструмент побудови графіків включає кілька попередньо визначених констант, які можуть спростити створення рівнянь. Ці константи:
piабоπ: Математична константа π (~3.14159).e: Число Ейлера (~2.71828).infinityабо∞, хоча вона рідко використовується для побудови кінцевих графіків.
Робота з рівняннями з кількома розвʼязками
Використання ± для симетричних розвʼязків
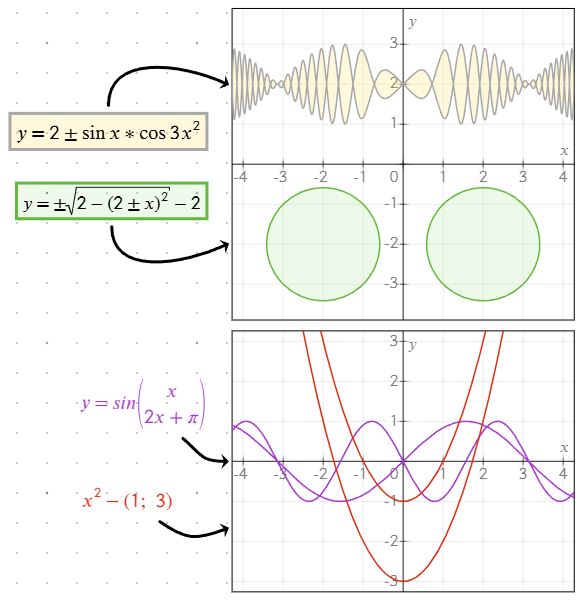
Вставте символ ± (або +-, який автоматично перетворюється на ±), щоб одночасно побудувати як додатні, так і від’ємні розвʼязки. Наприклад: y = ±sqrt(x) побудує і y = sqrt(x), і y = -sqrt(x).
Вказівка кількох значень
Ви можете вказати кілька значень або підрівнянь в одному об’єкті рівняння, використовуючи формат списку або кілька рядків:
- Списки в дужках: Використовуйте
;як роздільник у дужках, щоб вказати кілька значень. Наприклад:y = (1; -1) * xпобудує іy = x, іy = -x. - Окремі рядки: Натисніть Enter в редакторі рівнянь, щоб додати кілька підрівнянь на різних рядках. Кожен рядок розглядається як незалежний розвʼязок.
Ці методи дозволяють гнучко створювати графіки з кількома гілками або розвʼязками, спрощуючи візуалізацію складних взаємозв’язків.
Усунення проблем із побудовою графіків рівнянь
Якщо рівняння не відображається, це, ймовірно, через одну з таких причин:
- Помилка у синтаксисі рівняння (наприклад, відсутній оператор або недійсний символ).
- Діапазон змінної (наприклад,
xабоt) неправильно визначений або не вказаний. - Рівняння може бути невизначеним у деяких областях (наприклад, ділення на нуль).
Щоб вирішити ці проблеми:
- Перевірте ваше рівняння на наявність друкарських помилок або помилок форматування.
- Якщо ви вказали діапазон, переконайтеся, що інтервал є коректним і відповідає вашому рівнянню.
- Спробуйте повторно ввести рівняння, щоб переконатися, що всі символи й оператори введені правильно.
Якщо проблеми зберігаються, протестуйте рівняння окремо, щоб підтвердити його коректність.
Міркування щодо продуктивності
Під час роботи зі складними або динамічними графіками продуктивність може знижуватися. Щоб забезпечити плавність роботи, зверніть увагу на такі поради:
- Складні рівняння: Графіки з обчислювально складними обчисленнями (наприклад, вкладені тригонометричні функції або великі діапазони) можуть уповільнити рендеринг, особливо у поєднанні з анімацією.
- Швидкі коливання: Рівняння з високочастотними коливаннями (наприклад,
y = tan(1/x)) можуть бути неточно побудовані поблизу точок розриву через обмеження рендерингу. Щоб це зменшити, обмежте діапазон або спростіть рівняння, якщо це можливо. - Плавність анімації: Якщо ви використовуєте змінну
timeдля анімації, переконайтеся, що ваші рівняння не виконують надмірні обчислення для кожного кадру, щоб зберегти плавність руху.
Для найкращих результатів розгляньте можливість розбиття надто складних графіків на простіші компоненти або використання вужчих діапазонів для зменшення навантаження на обчислення.
Занадто багато графіків, видимих на екрані, також негативно впливають на продуктивність. Уникайте додавання надто багатьох графіків поруч, щоб забезпечити плавнішу роботу.