Graafiku tööriist võimaldab luua üksikasjalikke ja dünaamilisi graafikuid lihtsal ruudustikul. Koos võrranditööriistaga muutub see võimsaks võrrandite joonestamise tööriistaks, mis toetab Descartesi, polaarkoordinaatide ja parametrilisi võrrandeid.
Graafiku tööriist
Graafiku ruudustiku lisamine
Alustamiseks lisa oma tööruumile graafiku ruudustik:
- Klõpsa tööriistaribal nuppu Graafik (kiirklahv: H), et valida graafiku tööriist.
- Joonista tahvlile kast. Ilmub ruudustik koos x- ja y-teljega.
Sa võid ruudustikule käsitsi graafikuid joonistada, kuid see pole nii lõbus. Palju võimsam on joonestada sellele võrrandeid. Õpime kohe, kuidas seda teha.
Võrrandite joonestamine
Võrrandi joonestamiseks toimi järgmiselt:
- Kasuta võrranditööriista, et sisestada võrrand (nt y = 2x^3).
- Vali võrrand ja klõpsa tööriistariba valemisuvandites nuppu Joonesta võrrand (või ujuval tööriistaribal, kui see on lubatud). See loob graafiku objekti ja seob võrrandi graafikuga.
- Sisestatud võrrandi graafik joonestatakse automaatselt ruudustikule.
- Kui ruudustik on lisatud, saad seda suurendada või nihutada, et oma tööruumi paigutust kohandada.
Võrrandis tehtud muudatused kajastuvad graafikul koheselt. Samale graafikule saad joonestada mitu võrrandit, kui lingid need käsitsi graafikuga ühendustööriista abil.

Parameetrite vahemike määramine
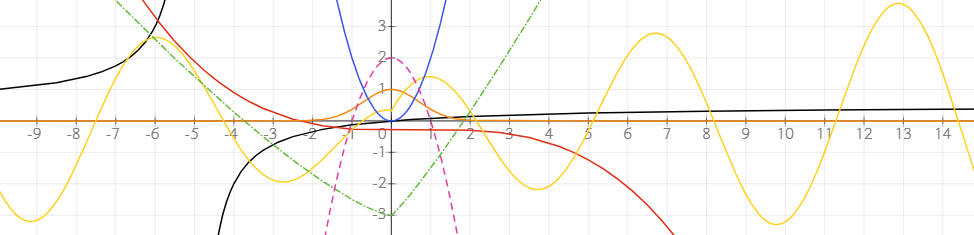
Sa saad määrata oma graafiku konkreetse vahemiku intervalli märgendiga. See võimaldab kontrollida graafiku joonestatud osa.
Sisesta vahemik võrrandina, näiteks x ∈ (-6; 2). Graafik piirdub määratud vahemikuga. Sümboli ∈ saamiseks kirjuta \in[space] või leia sümbol võrranditööriista menüüst.
Näiteks polaarkoordinaatides saad piirata nurkade vahemikku t ∈ (0; π), et joonestada poolring. Samuti saad parametriseeritud võrrandite puhul piirata parameetri vahemikku, et kuvada graafiku konkreetset segmenti.
Kui vahemikku ei määrata, kasutab tööriist muutuja või parameetri jaoks vaikimisi määratud piire, olenevalt graafiku tüübist. Näiteks Descartesi graafikute puhul sõltub x- ja y-vahemik graafiku objekti suurusest. Polaarkoordinaatides on muutujate vahemik 0 kuni 2π ja parametriseeritud võrrandite puhul on vahemik vaikimisi t ∈ (-5; 5).
Graafiku välimuse kohandamine
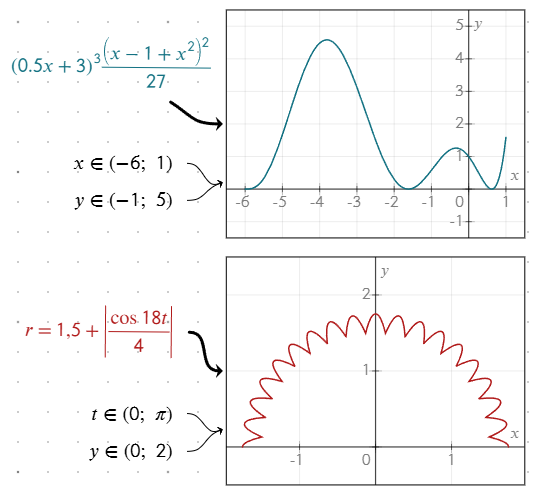
Sa saad graafiku joonte välimust kohandada, muutes võrrandi stiili:
- Lisa võrrandile ääris, et see vastaks graafiku joone stiilile.
- Muuda võrrandi teksti värvi, et kohandada joone värvi graafikul.
Kui äärist ei lisata, määrab teksti värv vaikimisi joone värvi.
Toetatud võrrandite tüübid
Graafiku tööriist toetab mitut tüüpi võrrandeid:
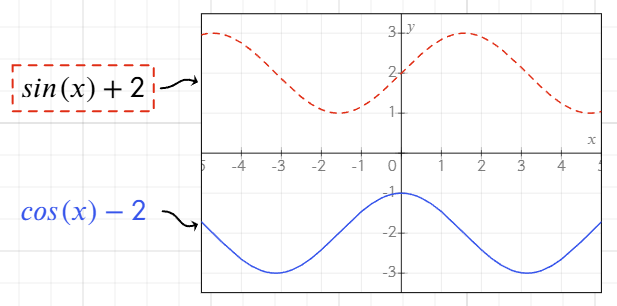
- Descartesi võrrandid: Kas
ykui funktsioonx-ist võixkui funktsioony-st. - Polaarsed võrrandid: Kasuta võrrandeid, mis arvutavad
rfunktsiooninat,thetavõiθ. Näiteksr = sin(t) + 2. Graafikud joonestatakse vahemikus[0, 2π]. Võrrand käitub sama moodi sõltumata sellest, mis nime muutuja kannab. - Parametriseeritud võrrandid: Määra
xjaysama parameetri funktsioonidena eraldi ridadel samas võrrandi objektis, näiteks:
x = 4 * sin(2t)
y = 3 * cos(3t)
Muutujate kasutamine võrrandites
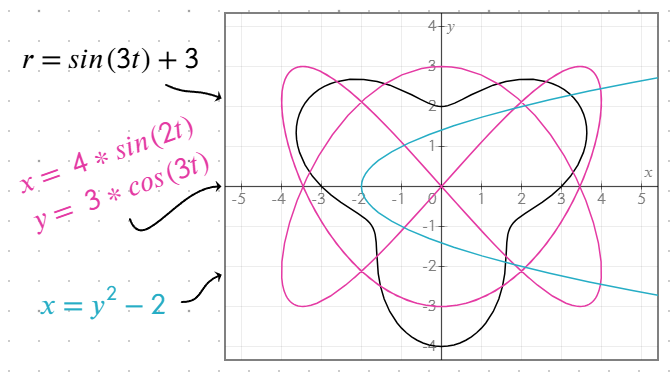
Sa saad võrrandites määrata muutujaid ja neid teistes uuesti kasutada. Näiteks: a = x^2, y = 0.2a - 1/a.
Graafik uueneb dünaamiliselt alati, kui muutujat või sõltuvaid võrrandeid muudetakse.
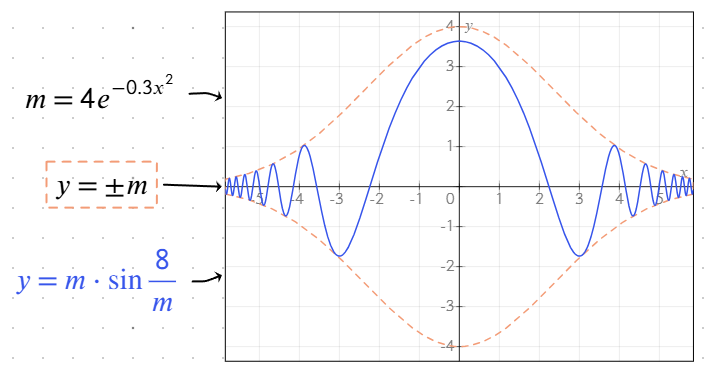
Toetatud funktsioonid
Graafikute tööriist sisaldab mitmeid sisseehitatud funktsioone, mis lihtsustavad võrrandite sisestamist ja parandavad visualiseerimist.
Trigonomeetrilised funktsioonid
- Standardsed:
sin,cos,tan,csc,sec,cot - Pöördfunktsioonid:
arcsin,arccos,arctan - Hüpterboolsed funktsioonid:
sinh,cosh,tanh,csch,sech,coth
Logaritmilised funktsioonid
log(x): 10-aluseline logaritmln(x): Looduslik logaritm (alusega e)
Muud funktsioonid
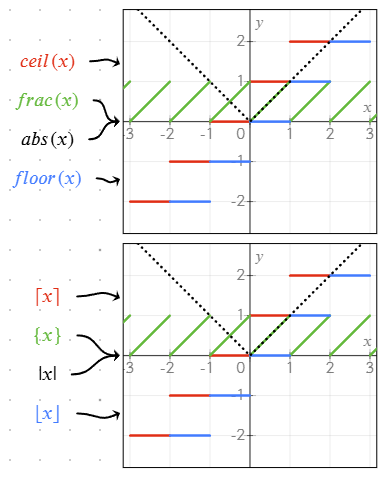
sqrt(x): Ruutjuurabs(x)või|x|: Absoluutväärtusfrac(x)või{x}: Arvu murdosafloor(x)või⌊x⌋: Ümardab alla lähima täisarvuniceil(x)või⌈x⌉: Ümardab üles lähima täisarvunimin(a; b),max(a; b): Väikseim/suurim kahest või enamast väärtusest
Neid funktsioone saab kombineerida võrrandites keerukamate graafikute ja arvutuste loomiseks.
Kohandatud funktsioonide määratlemine ja kasutamine
Graafikute tööriist võimaldab määratleda funktsioone, kasutades f(x) = ... märgendit, mis muudab avaldiste taaskasutamise erinevates võrrandites lihtsaks.
Funktsiooni määratlemiseks kasuta järgmist vormingut: f(x) = cos(2x) + sin(x)
Funktsioonide kasutamine võrrandites
Kui funktsioon on määratletud, saab seda kasutada teistes võrrandites: g(x) = f(x) + 5
Kui funktsioon on määratud kujul f(x) = ..., joonistatakse see graafikule. Muud variatsioonid (nt g(t)) ei joonistata, kuid neid saab kasutada arvutustes.
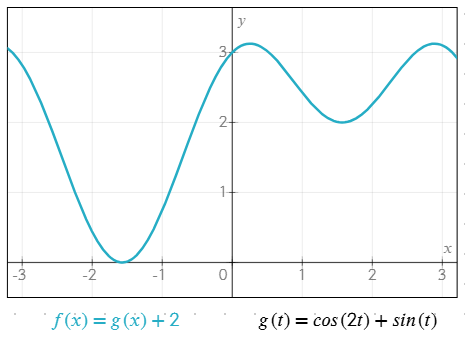
Näide mitme funktsiooni koos töötamisest
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Kohandatud funktsioonid aitavad lihtsustada võrrandeid, vältida kordusi ja hallata keerulisi avaldisi hõlpsamini.
Graafikute animeerimine 'time' muutujaga
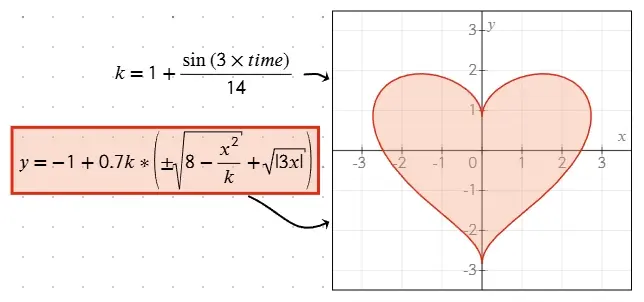
Kasuta spetsiaalset time muutujat, et luua animeeritud graafikuid. Muutuja time suureneb iga sekundiga ühe võrra, võimaldades simuleerida liikumist või perioodilisi muutusi võrrandites.
Näiteks: r = sin(5 * time) + 2 loob pulseeriva ringi, mis uueneb reaalajas.
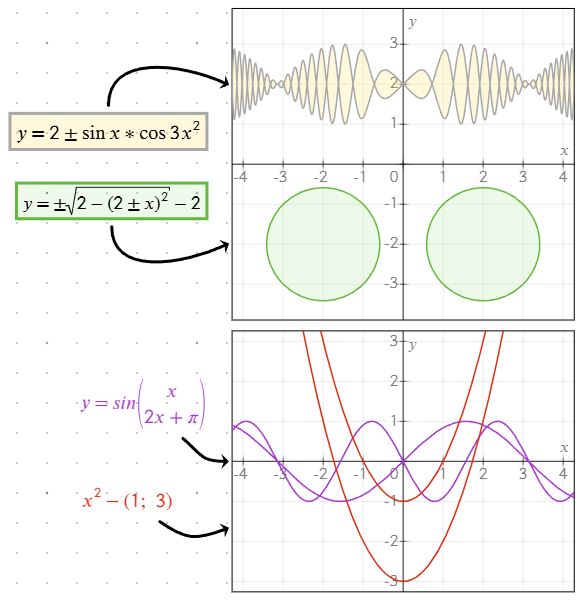
Parempoolsel pildil näed veidi keerulisemat võrrandit, mis kasutab ajamuutujat.
Eelmääratud muutujate kasutamine
Graafiku tööriist sisaldab mitmeid eelmääratud konstante, mis muudavad võrrandite loomise lihtsamaks. Need konstandid on:
pivõiπ: Matemaatiline konstant π (~3.14159).e: Euleri arv (~2.71828).infinityvõi∞, kuigi seda kasutatakse harva lõplike graafikute joonestamiseks.
Mitme lahendusega võrrandite käsitlemine
± sümboli kasutamine sümmeetriliste lahenduste jaoks
Lisa võrrandisse sümbol ± (või +-, mis teisendatakse automaatselt ±-ks), et joonestada samaaegselt nii positiivsed kui ka negatiivsed tulemused. Näiteks: y = ±sqrt(x) joonestab nii y = sqrt(x) kui ka y = -sqrt(x).
Mitme väärtuse määramine
Sa saad määrata mitu väärtust või osavõrrandit ühes võrrandi objektis, kasutades loendi vormingut või mitut rida:
- Loendid sulgudes: Kasuta
;eraldajana sulgudes, et määrata mitu väärtust. Näiteks:y = (1; -1) * xjoonestab niiy = xkui kay = -x. - Erinevad read: Vajuta võrrandiredaktoris Enter, et lisada mitu osavõrrandit eri ridadele. Iga rida käsitletakse sõltumatu lahendusena.
Need meetodid võimaldavad luua paindlikult graafikuid mitme haru või lahendusega, muutes keeruliste seoste visualiseerimise lihtsamaks.
Võrrandite joonestamise probleemide lahendamine
Kui võrrandit ei joonestata, on tõenäoline, et see tuleneb järgmistest põhjustest:
- Võrrandi süntaksis on viga (nt puuduv operaator või vale sümbol).
- Muutuja (nt
xvõit) vahemik on valesti määratud või pole määratud. - Võrrand võib olla mõnes piirkonnas olemuslikult määramatu (nt jagamine nulliga).
Nende probleemide lahendamiseks:
- Kontrolli oma võrrandit, et leida kirjavigu või vormindusvigu.
- Kui määrasid vahemiku, veendu, et intervall on kehtiv ja asjakohane sinu võrrandile.
- Proovi võrrand uuesti sisestada, et veenduda, et kõik sümbolid ja operaatorid on õigesti sisestatud.
Kui probleemid püsivad, testi võrrandit isoleeritult, et kinnitada selle kehtivust.
Jõudluskaalutlused
Komplekssete või dünaamiliste graafikutega töötamisel võib jõudlus halveneda. Sujuvama kogemuse tagamiseks pea meeles järgmist:
- Keerulised võrrandid: Graafikud, millel on arvutuslikult rasked kalkulatsioonid (nt keerulised trigoonomeetrilised funktsioonid või suured vahemikud), võivad renderdamist aeglustada, eriti animatsioonidega kombineerituna.
- Kiired ostsillatsioonid: Võrrandid, millel on kõrgsageduslikud ostsillatsioonid (nt
y = tan(1/x)), võivad nende murdepunktide lähedal olla ebatäpsed renderdamispiirangute tõttu. Selle vähendamiseks piira vahemikku või lihtsusta võrrandit, kui võimalik. - Animatsiooni sujuvus: Kui kasutad
timemuutujat animatsioonide jaoks, veendu, et sinu võrrandid ei teeks iga kaadri kohta liigseid ümberarvutusi, et säilitada sujuv liikumine.
Parimate tulemuste saavutamiseks kaalu liiga keeruliste graafikute jagamist lihtsamateks komponentideks või kitsamate vahemike kasutamist arvutuskoormuse vähendamiseks.
Liiga palju nähtavaid graafikuid ekraanil mõjutab jõudlust negatiivselt. Väldi liiga paljude graafikute lisamist samasse kohta, et tagada sujuvam töö.