Grafik aracı, basit bir ızgara üzerinde ayrıntılı ve dinamik grafikler oluşturmanıza olanak tanır. Denklem aracıyla birleştirildiğinde, Kartezyen, Polar ve Parametrik denklemler için güçlü bir grafik çizim aracı haline gelir.
Grafik Aracı
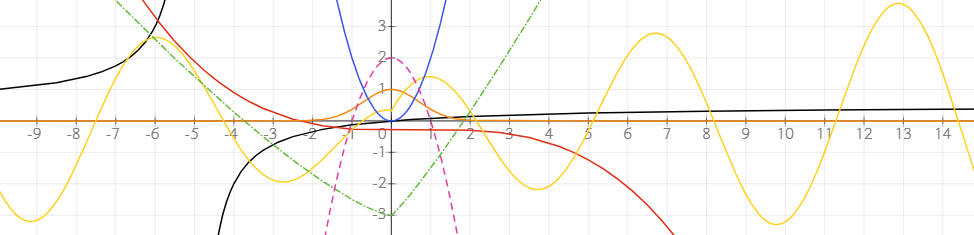
Grafik ızgarası ekleme
Başlamak için çalışma alanınıza bir grafik ızgarası ekleyin:
- Grafik aracını seçmek için araç çubuğundaki Grafik düğmesine tıklayın (kısayol: H).
- Tahta üzerine bir dikdörtgen çizin. x ve y eksenlerine sahip bir ızgara görünecektir.
Izgara üzerinde elle grafik çizebilirsiniz, ancak bu pek eğlenceli olmaz. Denklemleri üzerine çizmek çok daha güçlü bir yöntemdir. Bunu hemen nasıl yapacağımızı öğreneceğiz.
Denklem grafikleri çizme
Bir denklem grafiği çizmek için şu adımları izleyin:
- Denklem aracını kullanarak bir denklem girin (örneğin, y = 2x^3).
- Denklemi seçip araç çubuğundaki Formül seçeneklerindeki Denklemi çiz düğmesine tıklayın (veya etkinse kayan araç çubuğunda). Bu, bir grafik nesnesi oluşturur ve denklemi grafiğe bağlar.
- Yazdığınız denklemin grafiği otomatik olarak ızgara üzerinde çizilir.
- Izgarayı ekledikten sonra, çalışma alanı düzeninizi ayarlamak için ızgaranın boyutunu değiştirebilir veya taşıyabilirsiniz.
Denklemde yapılan değişiklikler grafikte anında yansıtılır. Ayrıca, bağlantı aracıyla grafiğe elle bağlayarak aynı grafik üzerinde birden fazla denklem çizebilirsiniz.

Parametre aralıklarını tanımlama
Grafiğiniz için belirli bir aralığı, aralık gösterimi kullanarak tanımlayabilirsiniz. Bu, grafiğin çizilecek kısmını kontrol etmenize olanak tanır.
Bir aralığı x ∈ (-6; 2) gibi bir denklem biçiminde girin. Grafik belirtilen aralıkla sınırlı olacaktır. ∈ sembolünü elde etmek için \in[boşluk] yazın veya denklem araç çubuğundan sembolü bulun.
Örneğin, polar koordinatlarda t ∈ (0; π) aralıklarını sınırlayarak bir yarım daire çizebilirsiniz. Benzer şekilde, parametrik denklemler için parametrenin aralığını sınırlayarak grafiğin belirli bir segmentini oluşturabilirsiniz.
Hiçbir aralık tanımlanmazsa, araç grafik türüne bağlı olarak değişken veya parametre için varsayılan sınırları kullanır. Örneğin, Kartezyen grafiklerde x ve y aralıkları grafik nesnesinin boyutuna bağlıdır. Polar grafiklerde değişkenin aralığı 0 ile 2π arasında, parametrik denklemlerde varsayılan aralık t ∈ (-5; 5) şeklindedir.
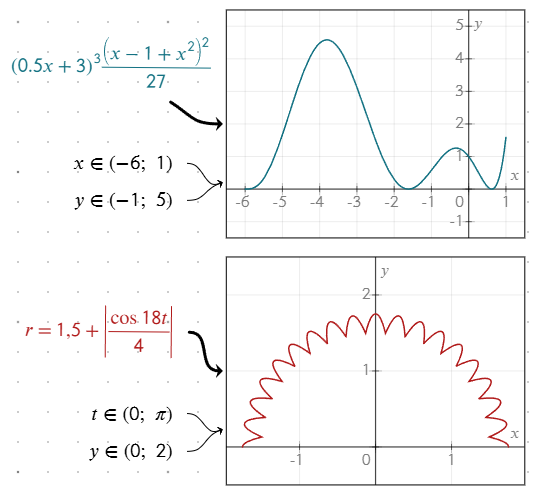
Grafik görünümünü özelleştirme
Denklemin görünümünü değiştirerek grafik çizgilerini stilize edebilirsiniz:
- Grafik çizgi stiline uyum sağlamak için denklem etrafına bir kenarlık ekleyin.
- Grafikteki çizginin rengini ayarlamak için denklem metninin rengini değiştirin.
Eğer kenarlık uygulanmazsa, metnin rengi varsayılan olarak çizgi rengini belirler.
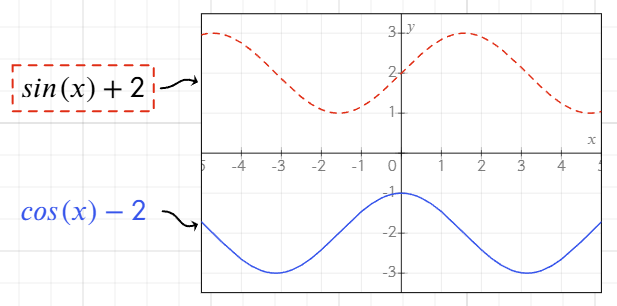
Desteklenen denklem türleri
Grafik aracı, çeşitli türde denklemleri destekler:
- Kartezyen denklemler:
y,x'in bir fonksiyonu olarak ya dax,y'nin bir fonksiyonu olarak. - Polar denklemler:
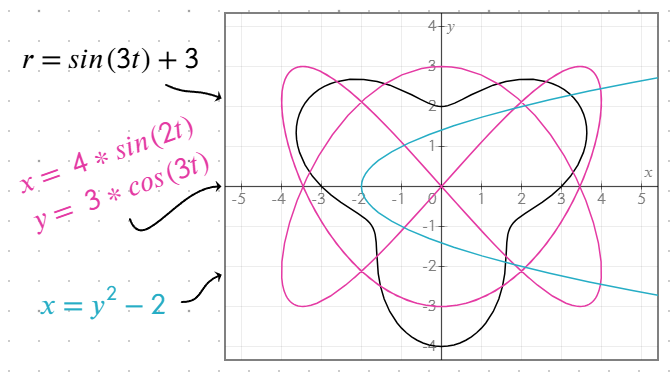
r,t,thetaveyaθ'nin bir fonksiyonu olarak hesaplayan denklemleri kullanın. Örneğin,r = sin(t) + 2. Grafikler[0, 2π]aralığında çizilir. Denklem, kullanılan değişkenin adına bakılmaksızın aynı şekilde davranır. - Parametrik denklemler: Aynı parametrenin fonksiyonları olarak
xvey'yi, aynı denklem nesnesi içinde ayrı satırlarda tanımlayın, örneğin:
x = 4 * sin(2t)
y = 3 * cos(3t)
Denklemlerde değişken kullanma
Denklemler içinde değişkenler tanımlayabilir ve bunları diğerlerinde yeniden kullanabilirsiniz. Örneğin: a = x^2, y = 0.2a - 1/a.
Grafik, değişken veya bağımlı denklemler değiştirildiğinde dinamik olarak güncellenir.
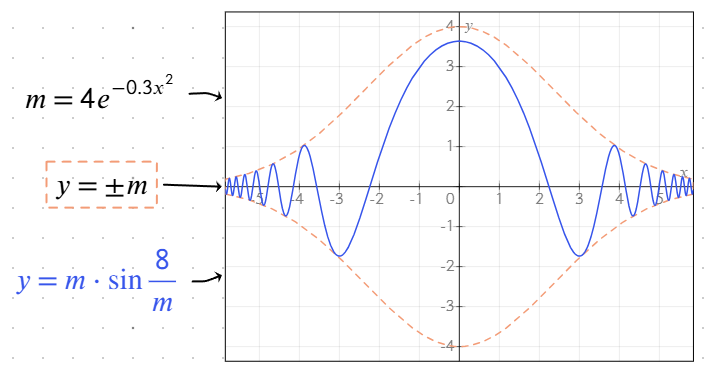
Desteklenen fonksiyonlar
Grafik çizim aracı, denklem girişini kolaylaştırmak ve görselleştirmeyi geliştirmek için çeşitli yerleşik fonksiyonlar içerir.
Trigonometrik fonksiyonlar
- Standart:
sin,cos,tan,csc,sec,cot - Ters (ark) fonksiyonlar:
arcsin,arccos,arctan - Hiperbolik fonksiyonlar:
sinh,cosh,tanh,csch,sech,coth
Logaritmik fonksiyonlar
log(x): 10 tabanında logaritmaln(x): Doğal logaritma (e tabanında)
Diğer fonksiyonlar
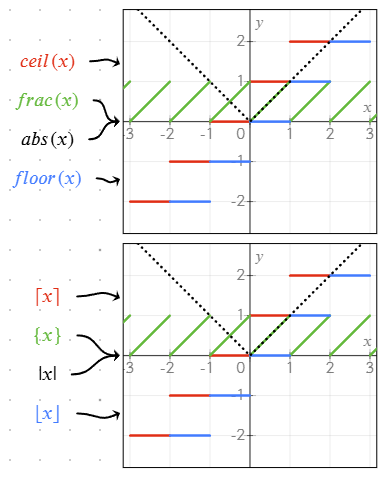
sqrt(x): Karekökabs(x)veya|x|: Mutlak değerfrac(x)veya{x}: Bir sayının kesirli kısmıfloor(x)veya⌊x⌋: En yakın tam sayıya aşağı yuvarlarceil(x)veya⌈x⌉: En yakın tam sayıya yukarı yuvarlarmin(a; b),max(a; b): İki veya daha fazla değerin en küçüğü/en büyüğü
Bu fonksiyonlar, daha karmaşık grafikler ve hesaplamalar oluşturmak için denklemler içinde birleştirilebilir.
Özel fonksiyonların tanımlanması ve kullanımı
Grafik çizim aracı, f(x) = ... notasyonunu kullanarak fonksiyon tanımlamayı destekler, böylece ifadeleri birden fazla denklemde yeniden kullanmayı kolaylaştırır.
Bir fonksiyon tanımlamak için şu formatı kullanın: f(x) = cos(2x) + sin(x)
Fonksiyonları denklemlerde kullanma
Tanımlandıktan sonra bir fonksiyon diğer denklemlerde referans alınabilir: g(x) = f(x) + 5
Eğer bir fonksiyon f(x) = ... olarak tanımlanırsa, grafik üzerinde çizilir. Diğer varyasyonlar (örneğin, g(t)) çizilmez ancak hesaplamalarda kullanılabilir.
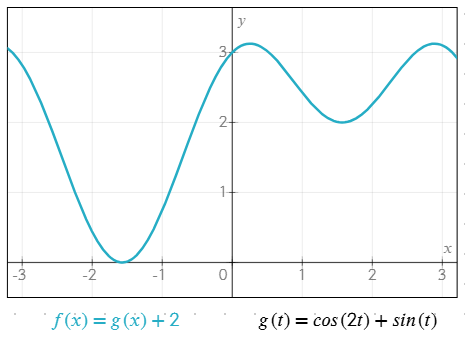
Birlikte çalışan birden fazla fonksiyon örneği
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Özel fonksiyonlar, denklemleri basitleştirmeye, tekrarları önlemeye ve karmaşık ifadeleri daha kolay yönetmeye yardımcı olur.
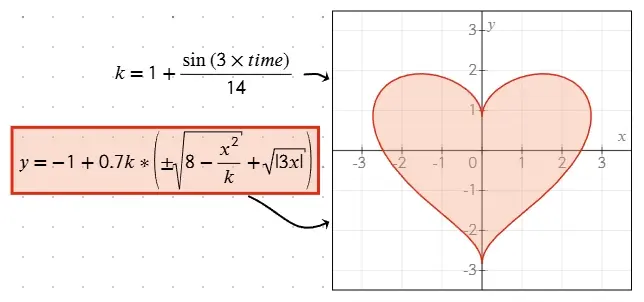
'time' değişkeni ile grafiklerin animasyonu
Animasyonlu grafikler oluşturmak için özel time değişkenini kullanın. time değişkeni her saniyede 1 artar ve bu, hareketi veya denklemlerinizdeki periyodik değişiklikleri simüle etmenize olanak tanır.
Örneğin: r = sin(5 * time) + 2, gerçek zamanlı olarak güncellenen nabız atan bir daire oluşturur.
Sağdaki resimde, zaman değişkenini kullanan biraz daha karmaşık bir denklem görebilirsiniz.
Önceden tanımlanmış değişkenlerin kullanımı
Grafik aracı, denklem oluşturmayı kolaylaştırabilecek birkaç önceden tanımlanmış sabit içerir. Bu sabitler şunlardır:
piveyaπ: Matematiksel sabit π (~3.14159).e: Euler sayısı (~2.71828).infinityveya∞, ancak bu genellikle sonlu grafikler için daha az kullanışlıdır.
Birden fazla çözümü olan denklemleri yönetme
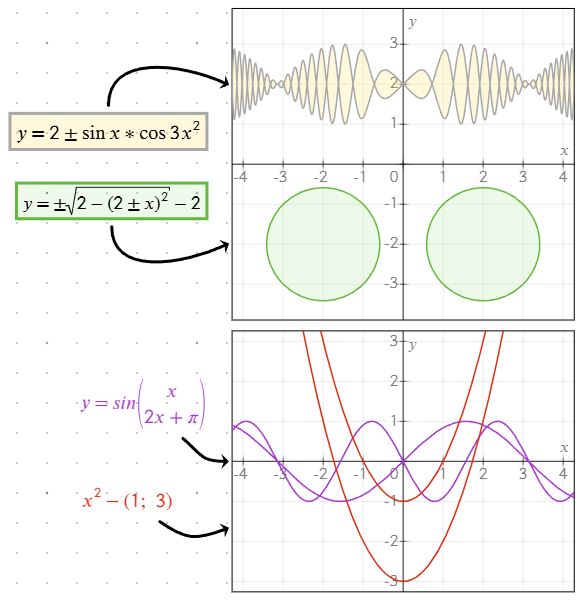
Simetrik çözümler için ± kullanımı
Hem pozitif hem de negatif sonuçları aynı anda çizmek için denkleme ± sembolünü (veya +-, ki bu otomatik olarak ±'ye dönüştürülür) ekleyin. Örneğin: y = ±sqrt(x), hem y = sqrt(x) hem de y = -sqrt(x) grafiklerini çizer.
Birden fazla değer belirtme
Bir denklem nesnesinde birden fazla değer veya alt denklem belirtebilirsiniz:
- Parantez içindeki listeler: Birden fazla değeri tanımlamak için parantez içinde
;ayırıcı kullanın. Örneğin:y = (1; -1) * xhemy = xhem dey = -xgrafiklerini çizer. - Ayrı satırlar: Denklem düzenleyicisinde Enter tuşuna basarak farklı satırlara birden fazla alt denklem ekleyin. Her satır bağımsız bir çözüm olarak ele alınır.
Bu yöntemler, birden fazla dalı veya çözümü olan grafiklerin esnek bir şekilde oluşturulmasına olanak tanır ve karmaşık ilişkilerin görselleştirilmesini kolaylaştırır.
Denklem grafiği çizim sorunlarını giderme
Bir denklem çizilemiyorsa, bu muhtemelen aşağıdaki nedenlerden biridir:
- Denklem sözdiziminde bir hata vardır (örneğin, eksik bir işlemci veya geçersiz bir sembol).
- Değişkenin (örneğin,
xveyat) aralığı yanlış tanımlanmış veya belirtilmemiştir. - Denklem, bazı bölgelerde doğası gereği tanımsız olabilir (örneğin, sıfıra bölme).
Bu sorunları çözmek için:
- Denklemdeki yazım hatalarını veya biçimlendirme hatalarını kontrol edin.
- Bir aralık belirttiyseniz, aralığın geçerli ve denklemle ilgili olduğundan emin olun.
- Denklemdeki tüm sembollerin ve işleçlerin doğru girildiğinden emin olmak için denklemi tekrar yazmayı deneyin.
Sorunlar devam ederse, denklemi izole bir şekilde test ederek geçerliliğini doğrulayın.
Performansla ilgili hususlar
Karmaşık veya dinamik grafiklerle çalışırken performans etkilenebilir. Akıcı bir deneyim sağlamak için aşağıdaki ipuçlarını aklınızda bulundurun:
- Karmaşık denklemler: Hesaplama açısından yoğun işlemleri olan grafikler (örneğin, iç içe trigonometrik fonksiyonlar veya geniş aralıklar), özellikle animasyonlarla birleştirildiğinde, render işlemini yavaşlatabilir.
- Hızlı dalgalanmalar: Yüksek frekanslı dalgalanmalara sahip denklemler (örneğin,
y = tan(1/x)) kırılma noktalarına yakın yerlerde, render sınırlamaları nedeniyle hatalı çizilebilir. Bunu azaltmak için aralığı sınırlayın veya mümkün olduğunca denklemi basitleştirin. - Animasyon akıcılığı: Animasyonlar için
timedeğişkenini kullanıyorsanız, her karede aşırı hesaplama yapılmadığından emin olun, böylece hareket akıcı kalır.
En iyi sonuçlar için, çok karmaşık grafiklerin daha basit bileşenlere bölünmesini veya hesaplama yükünü azaltmak için daha dar aralıklar kullanılmasını düşünün.
Ekranda çok fazla grafik olması da performansı olumsuz etkiler. Daha akıcı bir deneyim için birbirine yakın çok fazla grafik eklemekten kaçının.