Narzędzie do rysowania wykresów pozwala na tworzenie szczegółowych i dynamicznych wykresów na prostej siatce. W połączeniu z narzędziem do równań staje się potężnym narzędziem do rysowania wykresów równań z obsługą układów kartezjańskich, biegunowych i parametrycznych.
Narzędzie do rysowania wykresów
Dodawanie siatki wykresu
Aby rozpocząć, dodaj siatkę wykresu do swojego obszaru roboczego:
- Kliknij przycisk Wykres na pasku narzędzi (skrót: H), aby wybrać narzędzie do wykresów.
- Narysuj prostokąt na tablicy. Pojawi się siatka z osiami x i y.
Możesz ręcznie rysować wykresy na siatce, ale to nie jest zbyt zabawne. O wiele potężniejsze jest rysowanie wykresów równań na siatce. Zaraz dowiemy się, jak to zrobić.
Rysowanie wykresów równań
Aby narysować wykres równania, wykonaj następujące kroki:
- Użyj narzędzia do równań, aby wpisać równanie (np. y = 2x^3).
- Zaznacz równanie i kliknij przycisk Narysuj wykres w opcjach Formuły na pasku narzędzi (lub w pływającym pasku, jeśli jest włączony). Spowoduje to utworzenie obiektu wykresu i powiąże równanie z wykresem.
- Wykres równania, które wpisałeś, zostanie automatycznie narysowany na siatce.
- Po dodaniu siatki możesz ją zmieniać rozmiar lub przesuwać, aby dostosować układ obszaru roboczego.
Zmiany wprowadzone w równaniu są natychmiast odzwierciedlane na wykresie. Możesz również rysować wiele równań na tym samym wykresie, jeśli ręcznie połączysz je z wykresem za pomocą narzędzia do łączenia.

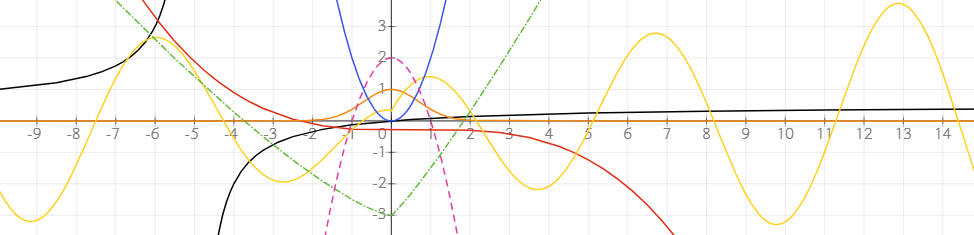
Definiowanie zakresów parametrów
Możesz zdefiniować określony zakres dla swojego wykresu za pomocą notacji przedziału. Pozwala to kontrolować, która część wykresu zostanie narysowana.
Wprowadź zakres w postaci równania, na przykład x ∈ (-6; 2). Wykres zostanie ograniczony do określonego zakresu. Aby uzyskać symbol ∈, wpisz \in[spacja] lub znajdź symbol na pasku narzędzi do równań.
Na przykład w układzie biegunowym możesz ograniczyć zakres kąta do t ∈ (0; π), aby narysować półokrąg. Podobnie, w przypadku równań parametrycznych możesz ograniczyć zakres parametru, aby uzyskać konkretny segment wykresu.
Jeśli nie zdefiniujesz zakresu, narzędzie użyje domyślnych granic dla zmiennej lub parametru w zależności od typu wykresu. Na przykład, w wykresach kartezjańskich zakresy x i y zależą od rozmiaru obiektu wykresu. W układzie biegunowym zakres zmiennej wynosi od 0 do 2π, a w równaniach parametrycznych zakres domyślny to t ∈ (-5; 5).
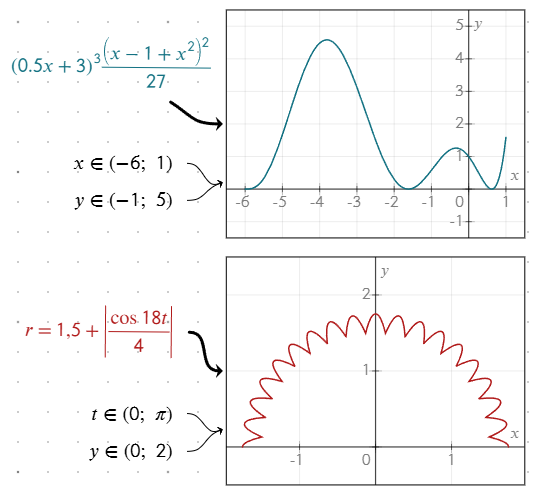
Dostosowywanie wyglądu wykresu
Możesz dostosować wygląd linii wykresu, zmieniając styl równania:
- Dodaj obramowanie wokół równania, aby dopasować styl linii wykresu.
- Zmień kolor tekstu równania, aby dostosować kolor linii na wykresie.
Jeśli nie zastosujesz obramowania, kolor tekstu domyślnie określi kolor linii.
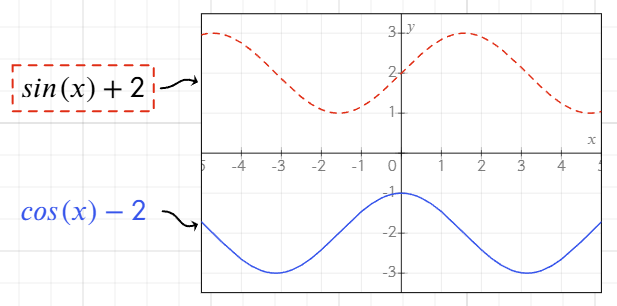
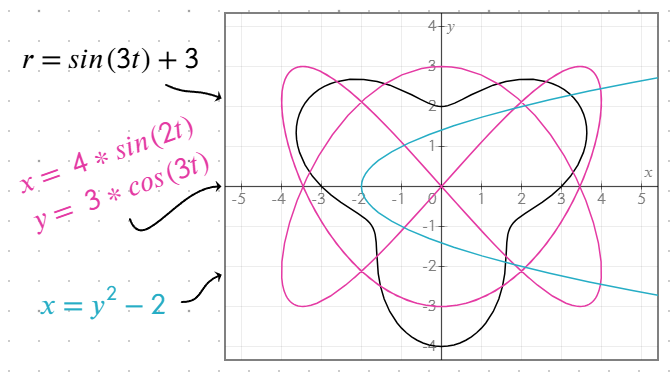
Obsługiwane typy równań
Narzędzie do wykresów obsługuje różne typy równań:
- Równania kartezjańskie:
yjako funkcjaxlubxjako funkcjay. - Równania biegunowe: Używaj równań obliczających
rjako funkcjęt,thetalubθ. Na przykładr = sin(t) + 2. Wykresy są rysowane w zakresie[0, 2π]. Równanie działa tak samo, niezależnie od nazwy użytej zmiennej. - Równania parametryczne: Zdefiniuj
xiyjako funkcje tego samego parametru w oddzielnych liniach w tym samym obiekcie równania, na przykład:
x = 4 * sin(2t)
y = 3 * cos(3t)
Używanie zmiennych w równaniach
Możesz definiować zmienne w równaniach i ponownie używać ich w innych. Na przykład: a = x^2, y = 0.2a - 1/a.
Wykres jest dynamicznie aktualizowany za każdym razem, gdy zmienna lub zależne równania są modyfikowane.
Obsługiwane funkcje
Narzędzie do tworzenia wykresów zawiera różne wbudowane funkcje, które upraszczają wprowadzanie równań i poprawiają wizualizację.
Funkcje trygonometryczne
- Standardowe:
sin,cos,tan,csc,sec,cot - Funkcje odwrotne (arcus):
arcsin,arccos,arctan - Funkcje hiperboliczne:
sinh,cosh,tanh,csch,sech,coth
Funkcje logarytmiczne
log(x): Logarytm dziesiętnyln(x): Logarytm naturalny (o podstawie e)
Inne funkcje
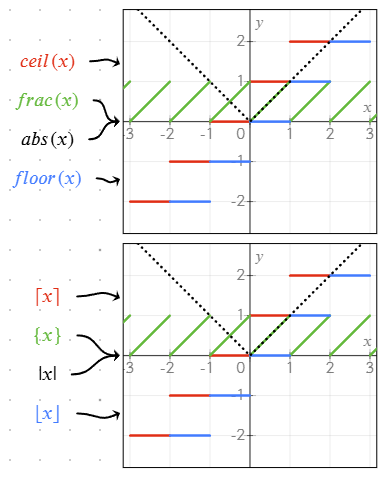
sqrt(x): Pierwiastek kwadratowyabs(x)lub|x|: Wartość bezwzględnafrac(x)lub{x}: Część ułamkowa liczbyfloor(x)lub⌊x⌋: Zaokrąglenie w dół do najbliższej liczby całkowitejceil(x)lub⌈x⌉: Zaokrąglenie w górę do najbliższej liczby całkowitejmin(a; b),max(a; b): Minimum/maksimum dwóch lub więcej wartości
Funkcje te można łączyć w równaniach, aby tworzyć bardziej złożone wykresy i obliczenia.
Definiowanie i używanie funkcji niestandardowych
Narzędzie do wykresów obsługuje definiowanie funkcji za pomocą notacji f(x) = ..., co ułatwia ponowne wykorzystanie wyrażeń w wielu równaniach.
Aby zdefiniować funkcję, użyj formatu: f(x) = cos(2x) + sin(x)
Używanie funkcji w równaniach
Po zdefiniowaniu funkcji można ją używać w innych równaniach: g(x) = f(x) + 5
Jeśli funkcja jest zdefiniowana jako f(x) = ..., zostanie wykreślona na wykresie. Inne warianty (np. g(t)) nie są wykreślane, ale mogą być używane w obliczeniach.
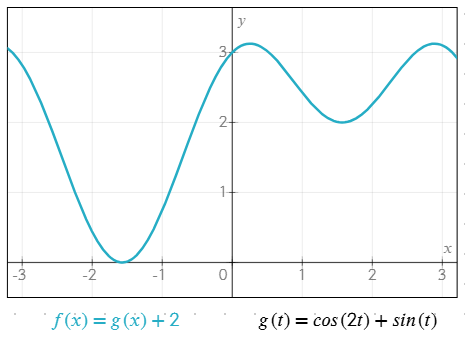
Przykład kilku funkcji współpracujących ze sobą
g(t) = cos(2t) + sin(t)f(x) = g(x) + 2
Funkcje niestandardowe pomagają upraszczać równania, unikać powtórzeń i ułatwiać zarządzanie złożonymi wyrażeniami.
Animowanie wykresów za pomocą zmiennej 'time'
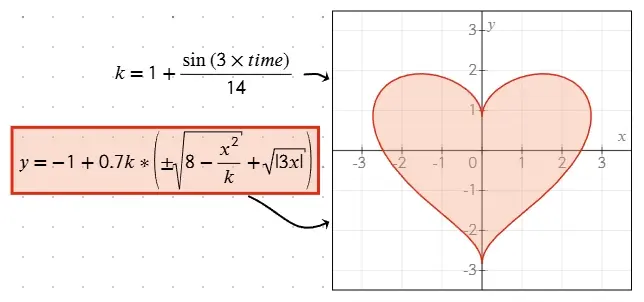
Użyj specjalnej zmiennej time, aby tworzyć animowane wykresy. Zmienna time zwiększa się o 1 każdą sekundę, co pozwala symulować ruch lub okresowe zmiany w równaniach.
Na przykład: r = sin(5 * time) + 2 tworzy pulsujący okrąg, który jest aktualizowany w czasie rzeczywistym.
Na obrazie po prawej stronie widać nieco bardziej złożone równanie wykorzystujące zmienną czas.
Korzystanie z predefiniowanych zmiennych
Narzędzie do wykresów zawiera kilka predefiniowanych stałych, które mogą uprościć tworzenie równań. Te stałe to:
pilubπ: Stała matematyczna π (~3,14159).e: Liczba Eulera (~2,71828).infinitylub∞, choć jest ona mniej przydatna do rysowania skończonych wykresów.
Obsługa równań z wieloma rozwiązaniami
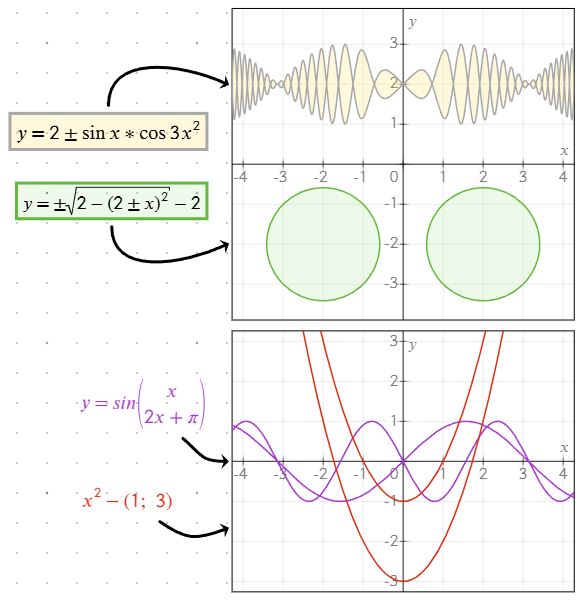
Używanie ± dla symetrycznych rozwiązań
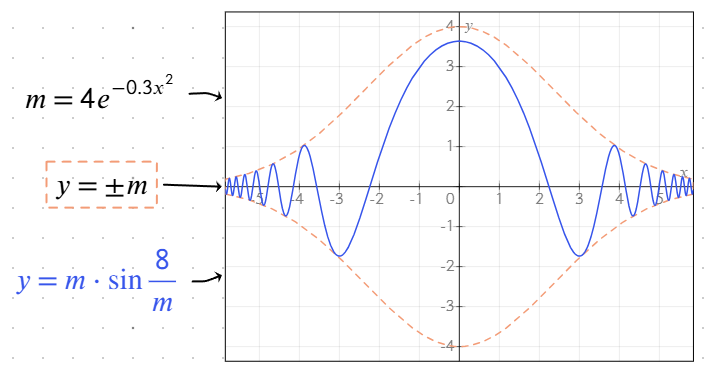
Wstaw symbol ± (lub +-, który zostanie automatycznie zamieniony na ±) do równania, aby jednocześnie rysować zarówno dodatnie, jak i ujemne wyniki. Na przykład: y = ±sqrt(x) narysuje zarówno y = sqrt(x), jak i y = -sqrt(x).
Określanie wielu wartości
Możesz określić wiele wartości lub pod-równań w jednym obiekcie równania, używając formatu listy lub wielu linii:
- Listy w nawiasach: Użyj
;jako separatora w nawiasach, aby zdefiniować wiele wartości. Na przykład:y = (1; -1) * xnarysuje zarównoy = x, jak iy = -x. - Oddzielne linie: Naciśnij Enter w edytorze równań, aby dodać wiele pod-równań na różnych liniach. Każda linia jest traktowana jako niezależne rozwiązanie.
Te metody pozwalają elastycznie tworzyć wykresy z wieloma gałęziami lub rozwiązaniami, ułatwiając wizualizację złożonych relacji.
Rozwiązywanie problemów z rysowaniem wykresów
Jeśli równanie nie jest rysowane, może to być spowodowane jednym z następujących powodów:
- Błąd w składni równania (np. brakujący operator lub nieprawidłowy symbol).
- Zakres dla zmiennej (np.
xlubt) został nieprawidłowo zdefiniowany lub nie został określony. - Równanie może być wewnętrznie niezdefiniowane w niektórych obszarach (np. dzielenie przez zero).
Aby rozwiązać te problemy:
- Sprawdź swoje równanie pod kątem literówek lub błędów formatowania.
- Jeśli określiłeś zakres, upewnij się, że przedział jest poprawny i odpowiedni dla twojego równania.
- Spróbuj ponownie wpisać równanie, aby upewnić się, że wszystkie symbole i operatory są poprawnie wprowadzone.
Jeśli problemy nadal występują, przetestuj równanie w izolacji, aby potwierdzić jego poprawność.
Uwagi dotyczące wydajności
Podczas pracy z złożonymi lub dynamicznymi wykresami wydajność może ulec pogorszeniu. Aby utrzymać płynne działanie, pamiętaj o następujących wskazówkach:
- Złożone równania: Wykresy z obliczeniami wymagającymi dużej mocy obliczeniowej (np. zagnieżdżone funkcje trygonometryczne lub szerokie zakresy) mogą spowolnić renderowanie, szczególnie w połączeniu z animacjami.
- Szybkie oscylacje: Równania z oscylacjami o wysokiej częstotliwości (np.
y = tan(1/x)) mogą być nieprecyzyjnie rysowane w pobliżu punktów krytycznych z powodu ograniczeń renderowania. Aby to zredukować, ogranicz zakres lub uprość równanie tam, gdzie to możliwe. - Płynność animacji: Jeśli używasz zmiennej
timedo animacji, upewnij się, że twoje równania nie wykonują nadmiernych obliczeń w każdej klatce, aby zachować płynność ruchu.
Aby uzyskać najlepsze wyniki, rozważ podzielenie zbyt złożonych wykresów na prostsze komponenty lub użycie węższych zakresów, aby zmniejszyć obciążenie obliczeniowe.
Zbyt wiele widocznych wykresów na ekranie również wpływa negatywnie na wydajność. Unikaj dodawania zbyt wielu wykresów blisko siebie, aby zapewnić płynniejszą pracę.